What is Abacus?
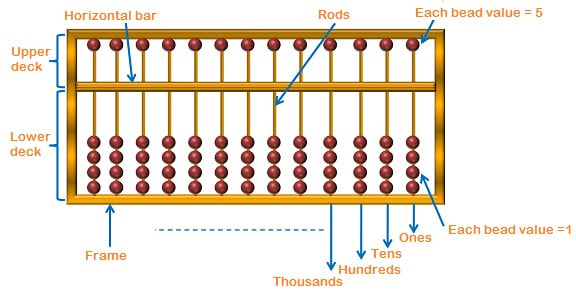
The Abacus is a simple yet powerful tool used for performing rapid arithmetic calculations. Invented in ancient times, it’s now widely adopted as a brain development program. The Abacus consists of a rectangular frame with vertically arranged rods, where beads slide up and down — representing numbers and place values.

Key Benefits of Abacus Learning
- ✅ One of the most popular calculating methods from ancient times.
- ✅ Helps children perform rapid calculations by visualizing bead movements.
- ✅ Studies show Abacus learners engage both brain hemispheres — left and right.
- ✅ Highly effective in improving children's concentration and memory levels.
What is Mental Arithmetic ?
Mental Arithmetic refers to performing mathematical calculations entirely in the mind — without the use of any physical tools like a calculator or paper. This skill is a key component of Abacus training, where learners visualize the movement of beads to solve problems quickly and accurately.
Benefits of Mental Arithmetic
- ✅ Enables rapid mental calculations, even with large numbers.
- ✅ Enhances imagination and visualization skills.
- ✅ Boosts performance in time-based competitive exams.
- ✅ Improves concentration, focus, and cognitive abilities.
What is the Soroban Method?
The Soroban Abacus is the traditional Japanese model of Abacus used for performing basic arithmetic operations. Apart from this model, a Chinese version of Abacus was used in ancient times which was called as Saunpan Abacus. The Suanpan is a horizontally structured Abacus that has 2 blocks. The upper block constitutes 2 beads and lower block constitutes 5 beads in each rod.

Why Learn the Soroban Method?
- ✅ Develops exceptional calculation speed and accuracy.
- ✅ Strengthens visualization and memory skills.
- ✅ Enhances problem-solving abilities and mental arithmetic.
- ✅ Promotes focus, concentration, and logical thinking.
Key factor of Soroban Method?
Mastering the Abacus, like any other skill, requires consistent practice. To become proficient, children should dedicate at least 30 minutes each day to practicing. After learning a new Abacus technique, it's essential to reinforce the lesson by practicing it for at least five days before moving on to the next one. This structured approach is why our Abacus centers hold classes once a week, allowing students ample time to absorb and master each concept before progressing.
Unlocking Mental Math with the Anzan Method
‘Anzan’ is a proven and highly effective technique for mastering mental Abacus calculations. This method emphasizes rapid visualization and mental math, turning math anxiety ("matho-phobia") into a love for numbers ("matho-philia"). AbacusMaster, a modern global Abacus education program, introduces Anzan as a fun and engaging way to practice, making math feel less like a chore and more like an exciting challenge.
Why Choose the Anzan Method?
- ✅ Develops rapid mental calculation skills.
- ✅ Strengthens visualization and memory power.
- ✅ Boosts focus, attention span, and listening skills.
- ✅ Transforms fear of math into confidence and enjoyment.
- ✅ Engaging video exercises with adjustable speed levels.
Anzan Learning Structure
| Level | Focus Area | Practice Time | Parent Monitoring |
|---|---|---|---|
| Level 1-2 | Basic Number Visualization | 15-20 mins daily | Ensure consistent practice |
| Level 3-4 | Speed & Accuracy Enhancement | 20-25 mins daily | Check video practice progress |
| Level 5-6 | Complex Multi-digit Operations | 30 mins daily | Monitor focus & speed improvement |
| Level 7-8 | Advanced Flash Anzan Training | 30+ mins daily | Track high-speed number solving |
🎯 Tip: AbacusMaster provides Anzan DVDs and online logins for students, allowing them to practice up to 8 levels at their own pace. Parents can easily monitor progress and ensure students stay consistent with their practice — all while having fun with number flash videos designed to improve speed and accuracy.
History of Abacus
Abacus is an ancient tool used invented to perform mathematical operations. It is still considered to be the most powerful calculating device, but can only be used by a trained abacus person. The definite origin of the abacus is obscure, there is some reason for believing that its earliest form was a reckoning table covered with sand or fine dust, in which figures were drawn with a stylus, to be erased with the finger when necessary.
The English word abacus is etymologically derived from the Greek abax, meaning a reckoning table covered with dust, which in turn comes from a Semitic word meaning dust or a reckoning table covered with dust or sand. In time this sanddust abacus gave place to a ruled table upon which counters or disks were arranged on lines to indicate numbers. Various forms of this line abacus were in common use in Europe until the opening of the seventeenth century. In rather remote times, a third form of abacus appeared in certain parts of the world. Instead of lines on which loose counters were laid, the table had movable counters sliding up and down grooves. All three types of abacuses were found at some time or other in ancient Rome —the dust abacus, the line abacus, and the grooved abacus. Out of this last type yet a fourth form of the abacus was developed—one with beads sliding on rods fixed in a frame. This form, the bead or rod abacus, with which calculations can be made much more quickly than on paper, is still used in China, Japan, and other parts of the world. In Europe, after the introduction of Arabic numerals, instrumental arithmetic ceased to make much progress and finally gave way altogether to the graphical as the supply of writing materials became gradually abundant.

As for the Orient, a form of the counting-rod abacus, called ch’eou in China and sangi in Japan, had been used since ancient times as a means of calculation. The Chinese abacus itself seems, according to the best evidence, to have originated in Central or Western Asia. There is a sixth-century Chinese reference to an abacus on which counters were rolled in grooves. The description of this ancient Chinese abacus and the known intercourse between East and West give us good reason to believe that the Chinese abacus was suggested by the Roman. The Chinese write in vertical columns from above downwards. If they ever are compelled to write in a horizontal line, they write from right to left. But the abacus is worked from left to right. This is another indication that the abacus was not indigenous to China. The present Chinese bead abacus, which is generally called suan-pan (arithmetic board) in Mandarin and soo-pan in the southern dialect, was a later development, probably appearing in the twelfth century, and did not come into common use till the fourteenth century. It is only natural that the people of the Orient, having retained a system of numerical notation unsuited for calculation, should have developed the abacus to a high degree, and its continuous universal use even after the introduction of Arabic numerals is eloquent testimony to the great efficiency achieved in its development. The Japanese word for abacus, soroban, is probably the Japanese rendering of the Chinese suan-pan. Although the soroban did not come into popular use in Japan until the seventeenth century, there is no doubt that it must have been known to Japanese merchants at least a couple of centuries earlier. In any case, once this convenient instrument of calculation became widely known in Japan, it was studied extensively and intensively by many mathematicians, including Seki Kowa (1640 — 1708), who discovered a native calculus independent of the Newtonian theory. As a result of all this study, the form and operational methods of the abacus have undergone one improvement after another. Like the present-day Chinese suan-pan, the soroban long had two beads above the beam and five below. But toward the close of the nineteenth century it was simplified by reducing the two beads above the beam to one, and finally around 1920 it acquired its present shape by omitting yet another bead, reducing those below the beam from five to four. Thus the present form of the soroban is a crystallization of labor and ingenuity in the field of Oriental mathematics and science. We feel sure that the soroban, enjoying widespread use in this mechanical age on account of its distinct advantages over the lightning calculating machine, will continue to be used in the coming atomic age as well.
Abacus Calculation Techniques
Basic Counting
Each bead represents a value. Lower beads (Earth beads) represent units, while upper beads (Heaven beads) represent fives. By sliding beads toward the beam, numbers are formed and calculated.
Addition & Subtraction
Add numbers by moving beads up toward the beam. Subtract by moving them away. For example, to add 7 and 5, first move 7, then add 5 more by adjusting the higher value beads.
Multiplication & Division
Multiplication is done by repeated addition, while division uses repeated subtraction. Abacus users often visualize this mentally after mastering the physical tool.
💡 Tip: Mastering these techniques improves both arithmetic speed and mental math abilities!
Mastering Abacus: Counting, Addition, Subtraction, and Division
The abacus is an amazing tool for fast calculations and improving mental math skills. Let’s dive into the essential techniques: counting, addition, subtraction, and division — with practical tricks and examples to help you master them!
1. Abacus Counting
Counting on an abacus is the foundation of all other operations. Each rod represents a place value (units, tens, hundreds, etc.). The lower beads (Earth beads) represent 1 each, and the upper beads (Heaven beads) represent 5 each.
🎯 Trick:
To count quickly, remember: - Each lower bead is 1 (move up). - Each upper bead is 5 (move down). - Move to the next rod when you hit 10.
✅ Example:
Count to 13 on the abacus: - Move 1 upper bead down (5). - Move 3 lower beads up (3). - 5 + 3 = 8. - Switch to the next rod and move 1 lower bead up for 10, add 3 more on the first rod — now you have 13!
2. Abacus Addition
Addition on an abacus is faster than you think — you just need the right technique.
🎯 Trick:
- Set the first number on the rods. - Add the second number by moving beads towards the center. - If a rod goes over 9, carry over to the next rod.
✅ Example:
Add 27 + 45: - Set 27 on the rods (2 on the tens rod, 7 on the units rod). - Add 4 to the tens rod (2 becomes 6). - Add 5 to the units rod (7 + 5 = 12 — carry over 1 to tens and leave 2 on units). - Final answer: 72.
3. Abacus Subtraction
Subtraction is just the reverse of addition, but it’s easier when you apply the trick.
🎯 Trick:
- Set the larger number on the rods. - Subtract by moving beads away from the center. - If you can’t subtract directly, borrow from the next rod (just like regular subtraction).
✅ Example:
Subtract 62 - 38: - Set 62 on the rods (6 on tens, 2 on units). - Subtract 3 from the tens rod (6 - 3 = 3). - Subtract 8 from the units rod — but 2 is too small, so borrow 1 from the tens rod (3 becomes 2) and add 10 to units (2 becomes 12). - Now subtract 8 from 12 — you’re left with 4. - Final answer: 24.
4. Abacus Division
Division on an abacus is like repeated subtraction — but faster.
🎯 Trick:
- Set the dividend (number to be divided) on the rods. - Subtract the divisor repeatedly, counting how many times you subtract. - If you can’t subtract anymore, the remaining beads are the remainder.
✅ Example:
Divide 36 ÷ 4: - Set 36 on the rods. - Subtract 4 repeatedly: - 36 - 4 = 32, 32 - 4 = 28, 28 - 4 = 24, 24 - 4 = 20... - Count how many times you subtract (9 times). - Final answer: 9, remainder 0.
✨ Why Use Abacus Techniques? ✨
Mastering abacus tricks boosts mental math, enhances concentration, and strengthens memory. Practice these tricks, and soon you’ll calculate faster than a calculator — all in your head!
📘 IELTS Preparation Guide
Your journey to mastering IELTS starts here with TutorX!
Why Prepare for IELTS?
Preparing for the IELTS exam requires a combination of strategy, consistency, and effective practice. Whether you're aiming for the Academic or General Training test, the key is to understand the test format, build strong English language skills, and practice under realistic conditions.
📍 Understanding the Four Sections
- Listening: Sharpen your skills with diverse accents and practice active listening.
- Reading: Focus on skimming for the main idea and scanning for details.
- Writing: Master task structure, use a variety of sentence structures, and expand your vocabulary.
- Speaking: Enhance fluency, pronunciation, and coherence with daily practice.
🛠️ Practice Strategy
Take full-length mock tests under timed conditions, review mistakes thoroughly, and improve. Remember, IELTS evaluates how well you communicate in real-world scenarios. Approach the test with confidence!
📅 7-Day Study Plan
| Day | Focus Area | Activity |
|---|---|---|
| 1 | Listening | Practice listening to different accents and complete a full test. |
| 2 | Reading | Read academic texts and summarize main ideas. |
| 3 | Writing | Practice Task 1 and Task 2. Review sample answers. |
| 4 | Speaking | Practice speaking on common topics. Record yourself. |
| 5 | Full Test | Take a complete IELTS test under timed conditions. |
| 6 | Weak Areas | Focus on the weakest section from Day 5. |
| 7 | Final Prep | Light review and relaxation before the exam day. |
🚀 Start with TutorX!
Get ready to ace your IELTS exam with expert guidance and proven strategies.
.png) Enrollment Form
Enrollment Form
.png)
.png)